音律の求め方と完全音程と音程の転回で長短変わる理由の解説
昨日の音楽理論講義で完全音程と音の転回時に長短が変わる理由について質問を受けましたので詳細に回答します。
完全音程は協和しているから、、、
音は転回した場合、そのその2音を足して9になり、長短逆になる、、、
ではその理由は?
何か明確な法則があるのでは?
そこを解説してくれとの要望に応えます。
<完全音程定義>
2音間の振動数比が単純な整数比で,協和度の高い音程
完全1度,完全4度,完全5度,完全8度などがある
Cを基準にすれば
CとC 完全1度(同音)
CとF 完全4度
CとG 完全5度
CとC 完全8度(オクターブ上)
となります。
(上記の音程は、“全音階的音程”の中の“協和音程”の中の“完全共和音程”に分類される)
さらに詳細に解説するために音律の求め方を純正律で解説します。
音律の求め方を純正律で解説
純正律とは
周波数の比が単純な整数比である純正音程のみを用いて規定される音律(下図を参照)(純正律は12平均律の基となっています)
純正律の音階表
| 音階名 | C | D | E | F | G | A | B | C |
| 周波数 | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 |
| セント | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 |
音階が1オクターブ上がると周波数は2倍、逆に1オクターブ下がれば1/2となります。
純正律の音階の決め方は倍音から計算式で求められています。
以下は倍音の表、第5倍音までです
| 倍音 | 音程 | 音名 |
| 第1倍音 | ユニゾン | C3 |
| 第2倍音 | 1オクターブ | C4 |
| 第3倍音 | 1オクターブと完全5度 | G4 |
| 第4倍音 | 2オクターブ | C5 |
| 第5倍音 | 2オクターブと長3度 | E5 |
この後理論上は終わりなく続きます。
倍音が倍になると周波数が倍になります。
最初に基音(今回はC)以外の音階が現れるのは第3倍音でオクターブ上のGです。
オクターブ外にあるため、1オクターブ下げます。
3/1 x 1/2
で3/2です。
これがオクターブ内にあるGの音(5度上)となります。
次に5度下も見てみましょう。
基音:五度下の音= 3/2 : 1 = 1 : 2/3
ですので5度下の音は基音の2/3倍、基音と同じオクターブ内に持って来るために倍にすると
2/3 x 2
で4/3になります。
この音が第4音Fの音になります。
次に基音以外の音が現れるのは第5倍音です。
2オクターブ上ですので1/4にします。
5 x 1/4
で5/4です。
これが第3音 E になります。
あとは組み合わせて残りのオクターブ内の音を導きます。
第5音の三度上が第7音B
第7音= 3/2 × 5/4 = 15/8
第4音の三度上が第6音 A
第6音= 4/3 × 5/4 = 5/3
第5音の五度上を1オクターブ下げて第2音 D
第2音= 3/2 × 3/2 × 1/2 =9/8
以上で7音が出揃いました。
| 音階名 | C | D | E | F | G | A | B | C |
| 周波数 | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 |
ではこの純正律の解説を踏まえて完全音程についてです。
完全音程とは
音は、同時に鳴った際に周波数比が小さな数でシンプルな比率の方が、協和性が高いと言えます。
上述の図にある通り、Cに対し基音C(1度)とオクターブ上のC(8度)の次に、FとG(第4音と、第5音)が4/3、3/2ともっともシンプルな比率となっています。
これらの音程はもっとも協和していると言えるでしょう。
この4音を完全音程(完全協和音程)と言います。
より明確に確認するために周波数を図にして見てみましょう。
まずは基音と1オクターブ上の音から
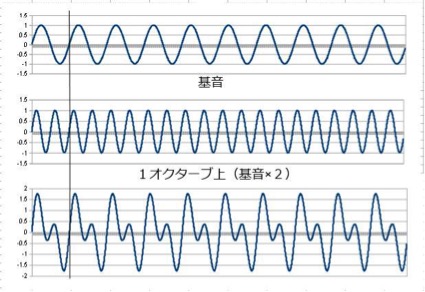
基音と同じ音(完全1度=同音)が周波数が同じになるのは当然として、オクターブ上の周波数も協和します。
1番下の波形が2つの音(基音とオクターブ上)を合わせた音です。
短い周期、かつ一定の周期で並んでいるため、音が協和している状態、完全協和音程の状態です。
次が残りの完全音程(完全協和音程)の2音
5度上と4度上です。
5度上
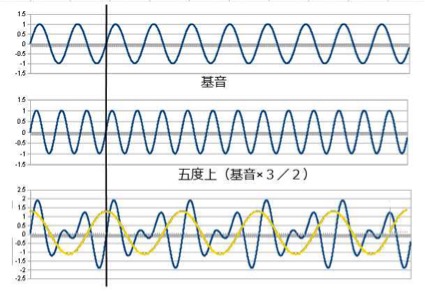
4度上
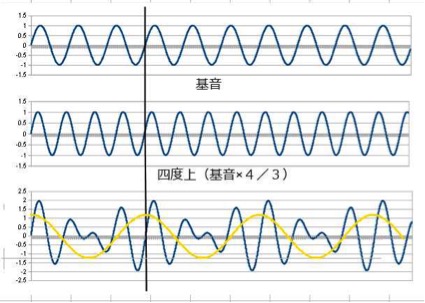
同じくそれぞれ1番下の重なった波形。
先ほどの基音+オクターブ上よりは周期が長くはなりますが、規則性があり協和している事が確認できます。
5度の方が4度よりも周期が短い=より協和している事も確認していただけるでしょう。
ここまでが完全音程です。
(ちなみに黄色の線は差音と言います。
差音については(説明がさらに長くなりますので)また次の機会に解説させていただきます。)
では、他の音はどうなのでしょうか?
3度上です。
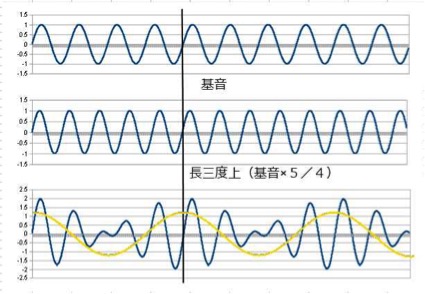
完全協和音程の5度、4度に比較すると、周期が長く、協和度が低い事が確認できます。
6度上です
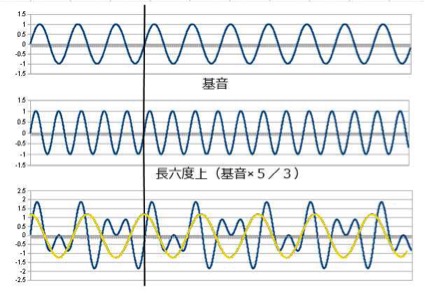
3度よりも周期が短く協和していると言えます。
しかし完全協和音程ではありません。
以上3度、6度に加えそれぞれを転回した際にできる(転回は後に解説)短3度、短6度の4音を不完全協和音程と呼びます。
短3度

短6度

残りの2度上と7度上です。
この2音は不協和音と呼ばれます。
2度上

かなり周期が長く協和はしていない感じが見て取れますね。
次は
7度上です
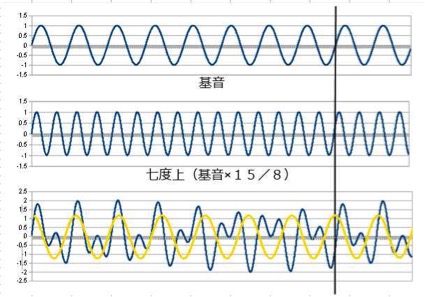
こちらも周期は長く、形はより複雑です。
以上の事から1度、4度、5度、8度は協和している音程で完全音程と呼ばれる事が確認できました。
次に音の転回の話です。
音の転回の解説
何故、転回すると長短変わるのか?
同時に完全音程が転回しても長短変わらない=完全である。についても解説します。
先ほど、音階の決め方の解説をしましたが、4度を決めるときに5度下の音程を基に決めていました。
次の表を見てください。
| 度数名 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 周波数 | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 |
| オクターブ下に転回 | 1/1 | 8/9 | 4/5 | 3/4 | 2/3 | 3/5 | 8/15 | 1/2 |
| 度数名 | 1 | 7b | 6b | 5 | 4 | 3b | 2b | 1 |
| オクターブ上げて周波数を調べる | 1 | 16/9 | 8/5 | 3/2 | 4/3 | 6/5 | 16/15 | 1 |
オクターブ下になった音をそれぞれオクターブ上にあげて同じオクターブ内の音階にします。
すると、完全音程である、1度、4度、5度、8度以外の音程(度数)は元の純正律にあった7音の中にありません。
逆にいうと、1度、4度、5度、8度は転回しても7音の音階に含まれている。
逆からみてもなくならずしっかりと残る。やはりここでも完全に存在する=完全音程と言える事がわかります。
2度下、3度下、6度下、7度下の音程は、オクターブ上に上げると、それぞれの対応する(2度は7度、3度は6度)短音程を構成する事となり12音階が出来上がります。
転回する事で長短が変わる事が確認できました。
ちなみにこれが12音

これを転回させると下図でわかる通り、5、6、7は長短変わらず(つまり完全音程)1〜4半音程は奇数が短音程から長音程、偶数が長音程から短音程、8〜11は奇数が長音程から短音程、偶数が短音程から長音程へと変化します。

なお転回した音程は度数を足すと9になり長短入れ替わるとともに、半音数の合計は12となります。
例:短2度の転回形は長7度=足すと度数は9、長短は入れ替わり。短2度は1半音、長7度は11半音で足すと12半音。
なお、純正律は、12平均律(今の機能和声)の基となりましたが、周波数は少々異なります。
12平均律は純正な周波数にはなっていないため、実はそもそも完全な協和音程とはなってはいません。
その事も知識として覚えておいていただければと思います。
| 音階名 | C | D | E | F | G | A | B | C |
| 純正律の周波数 | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 |
| 純正律の周波数を数字 | 1 | 1.125 | 1.250 | 1.333 | 1.5 | 1.666 | 1.875 | 2 |
| 平均律周波数を数字で | 1 | 1.122 | 1.260 | 1.355 | 1.498 | 1682 | 1.888 | 2 |
| 純正律との差 | 0 | 0.003 | 0.010 | 0.002 | 0.002 | 0.016 | 0.013 | 0 |
完全音程1、8度では差はなく、4、5度においても差はわずかである事が確認できます。

