ディープラーニングではバックプロパゲーション(誤差逆伝播)によりトレーニングデータの出力値と正解データとの誤差をなくす事によってモデルを作成します。
その際の誤差を求める方法(数式)はいくつかあるのですが、今回は回帰問題(Regression)で使用される基本の数式を2つ紹介します。
(コードはJupyter NotebookやGoogle Colab Notebookで同様に実行していただけます)
二乗和誤差
二乗和誤差(Mean Squared Error)は、もっともシンプルで最も使用されている損失関数でしょう。
機械学習を学ぶ際、最初に学ぶ損失関数はこの二乗和誤差だと思います。
canplayの講義でも最初にお教えするのはこの二乗和誤差です。
二乗和誤差の計算は、出力値と正解データデータの差を二乗し、データセット全体で平均します。
データセット全体で平均する(1/Nをかける)代わりに(微分しやすさのために)1/2をかける場合もあります。
二乗するのは誤差を必ず正の値にするためです。
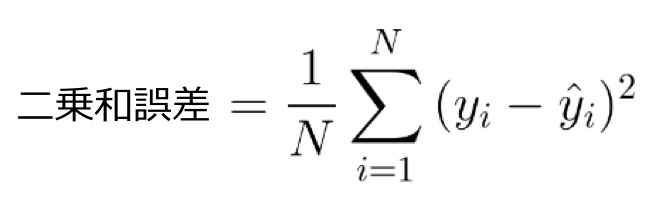
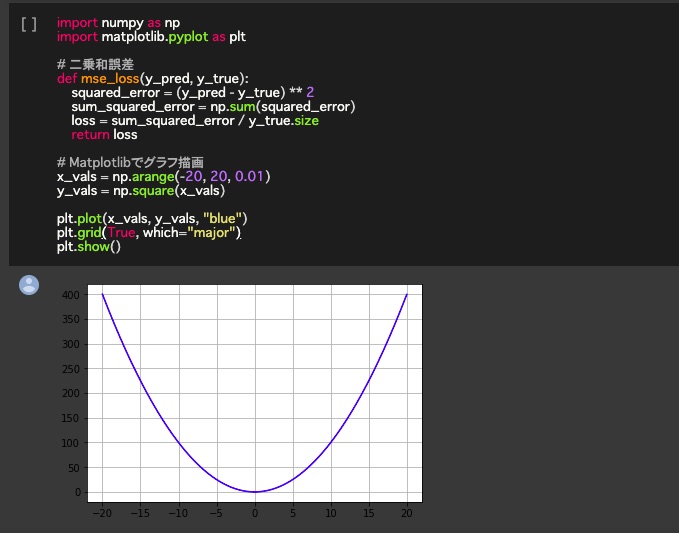
下記コードを実行しています。
誤差をなくす(0に近づける)ために学習を繰り返すわけですね。
import numpy as np
import matplotlib.pyplot as plt
# 二乗和誤差
def mse_loss(y_pred, y_true):
squared_error = (y_pred – y_true) ** 2
sum_squared_error = np.sum(squared_error)
loss = sum_squared_error / y_true.size
return loss
# Matplotlibでグラフ描画
x_vals = np.arange(-20, 20, 0.01)
y_vals = np.square(x_vals)
plt.plot(x_vals, y_vals, “blue”)
plt.grid(True, which=”major”)
plt.show()
長所と短所
二乗する事により必ず正の値になるだけでなく、大きな誤差をより大きく取り扱います。
よって学習済みモデルに大きな誤差が含まれる可能性をより少なくする事ができます。
ただし誤差がゼロに近づくにつれその誤差は小さく扱われますので精度を求められるモデルへの学習には向かないとも言えます。
平均絶対誤差
平均絶対誤差(Mean Absolute Error)の数式は二乗和誤差と見た感じは似ています。
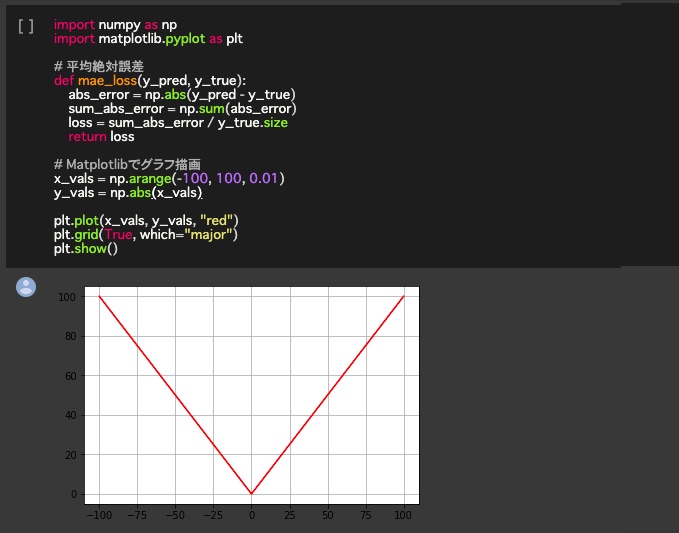
平均絶対誤差は、出力値と正解データのとの差を取り、その差に絶対値を適用してから、データセット全体で平均します。
つまり二乗和誤差との違いは差を二乗するのではなく、常に絶対値にする点です。
絶対値をとっているので、すべての誤差は同じ(直線の)線形スケールで重み付けされます。
二乗和誤差と違い、モデルのパフォーマンスを均一に評価できます。
import numpy as np
import matplotlib.pyplot as plt
# 平均絶対誤差
def mae_loss(y_pred, y_true):
abs_error = np.abs(y_pred – y_true)
sum_abs_error = np.sum(abs_error)
loss = sum_abs_error / y_true.size
return loss
# Matplotlibでグラフ描画
x_vals = np.arange(-100, 100, 0.01)
y_vals = np.abs(x_vals)
plt.plot(x_vals, y_vals, “red”)
plt.grid(True, which=”major”)
plt.show()
長所と短所
どの誤差の扱いも均一であるため、各モデル同士の比較などに有効です。
ただし、その事は(単一のモデル中の)誤差の違いを判別しにくいため、誤差の少ない(ゼロに近づいている)状態を把握しずらかったり、時に大きな誤差を含んだモデルを作成してしまったりします。
記事投稿日:2019/6/2

